【算法】非典型牛顿迭代法

何为牛顿迭代法

牛顿迭代法的全名叫做牛顿-拉夫森方法（Newton-Raphson method），这是一种在实数域和复数域上近似求解方程的方法。方法使用函数 $f(x)$ 的泰勒级数的前面几项来寻找方程 $f(y) = 0$ 的根。

对于一般的形如 $f(x) = 0$ 的方程，首先任意估算一个解$x1 $，一般来说此时不能得到方程的正确解，则我们在方程曲线上$ x=x_1 $处作$ f(x) $的切线，与x轴相交于点$ (x_2,0) $，此时$ x_2 $要更加接近于方程$ f(x)=0 $的解了。只要以此方式不断地更新$ x{n+1}$，就能无限接近于方程的精确解。

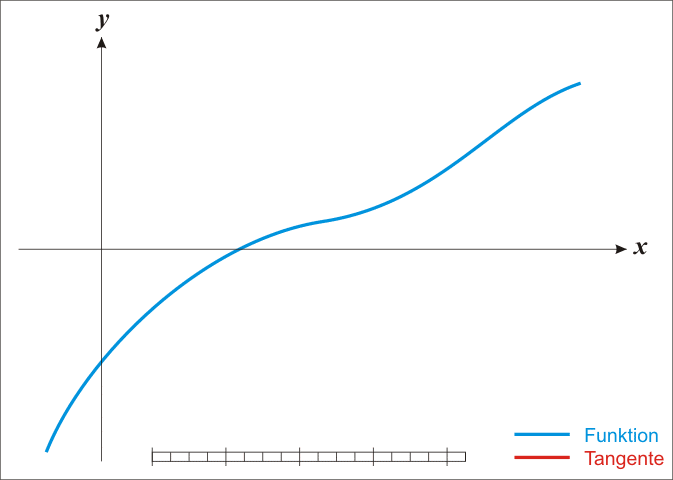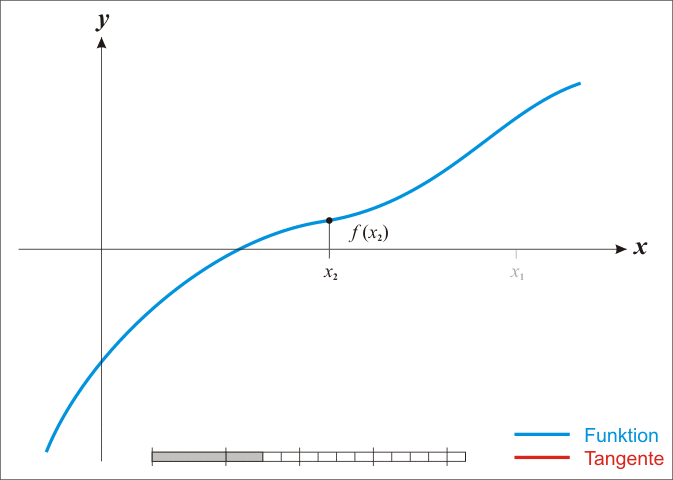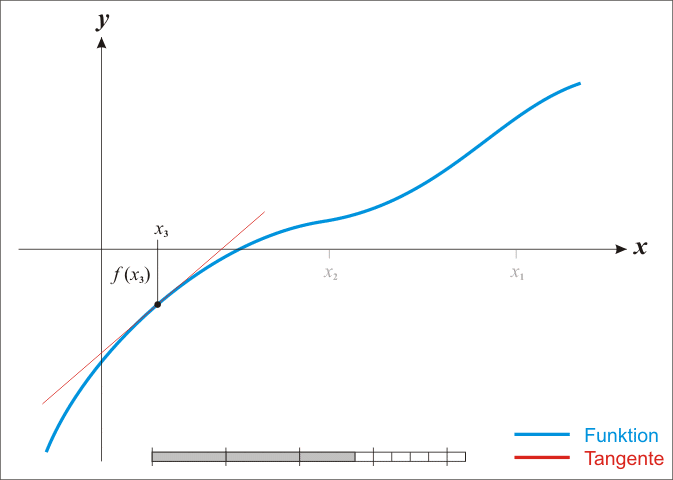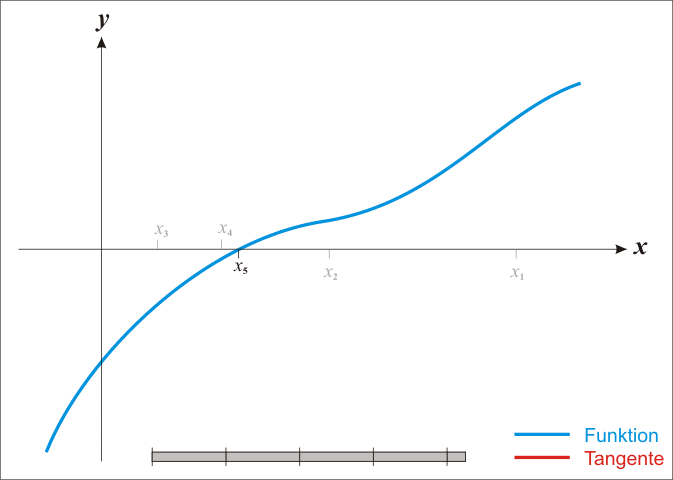
值得注意的是，该方法在函数不连续或者函数有多个零点的时候会失效。

代码实现

牛顿迭代法多用于以最快速度求一个数字 $m$ 的方根，仅需几次的迭代就能够得到非常精确的结果，下面举例来介绍牛顿迭代法求平方根的数学公式和实现。

不妨令 $x^m=n$ ，则方程为 $f(x) = x^m-n$ .

有

$f'(x)=mx^{m-1}$

$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=(1-m)x_n+\frac{nx_n}{mx_n^m}$

假设我们输入一个数字 $n$ ，我们现在需要求它的平方根 $x$ ，则

$f(x)=x^2-n$

$f'(x)=2x$

$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=\frac12(x_n+\frac{n}{x_n})$

则我们的迭代方程就是 $x_{n+1}=\frac{x_n}{2}+\frac{n}{2x_n}$ 。

现在要确定的是迭代终止条件，假设我们要求的精度是 $0.00001$ ，则迭代终止的条件为 $|x^2-n|<0.00001$ 。

由于 $x=0$ 的时候， $n$ 的值就为 $0$ ，所以我们将迭代的起点设置为 $x=1$ ，所以我们的程序如下：

#Python3
def mySqrt(self, n: int) -> float:
    if n == 0 or n == 1:
        return n
    #先处理特殊值
    x0 = 1.0
    ran = abs(x0 * x0 - n) #迭代停止信号
    while ran > 0.00001:
        x1 = x0 / 2 + n / (x0 * 2)
        x0 = x1
        ran = abs(x1 * x1 - n)
    return x1

当我们输入的值为2147395599时，输出46339.99998，输出耗时为32ms。而Python自带的n**0.5耗时60ms。

非典型算法

这里不得不提到神秘数字0x5f3759df，这个数字首次出现在游戏《雷神之锤III》的源代码中。

在一个名为q_math.c的文件里出现了如下代码

//C
float Q_rsqrt( float number ) { 
   	long i; float x2, y; const float threehalfs = 1.5F;
    x2 = number * 0.5F; 
    y = number; 
    i = * ( long * ) &y; // evil floating point bit level hacking 
    i = 0x5f3759df - ( i >> 1 ); // what the fuck? 
    y = * ( float * ) &i; 
    y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration 
    // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
    #ifndef Q3_VM #
    ifdef __linux__ assert( !isnan(y) ); // bk010122 - FPE?
    #endif
    #endif return y; 
 }

里面出现了一句让人抓毛的代码：

1	i = 0x5f3759df - ( i >> 1 ); // what the fuck?

这句代码和下面的两行一起

1
2
3

i = 0x5f3759df - ( i >> 1 ); // what the fuck? 
y = * ( float * ) &i; 
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration

就相当于求平方根的操作。

但其中的原理是什么，答案恐怕连写这个代码的人自己也不知道。（what the f*ck?）

参考

【1】维基百科：牛顿法

【2】力扣题目：求平方根